Considérations physiques autour du spin-casting

Le spin-casting (ou moulage par centrifugation) est une technique utile lorsque l'on souhaite créer une couche parfaitement circulaire dans un tube parfois non circulaire. Typiquement une couche d'isolation au centre de son moteur à ergols solides. L'excellent Joe Barnard l'a utilisé exactement à cet effet.

Vous avez dit parfaitement ?

Une pensée vient donc à l'esprit de tout bon physicien : comment cette technique peut-elle prétendre créer une couche uniforme ? Placé parfaitement à l'horizontale, il y aura sûrement plus de matière sur le bas du tube que le haut du tube ?

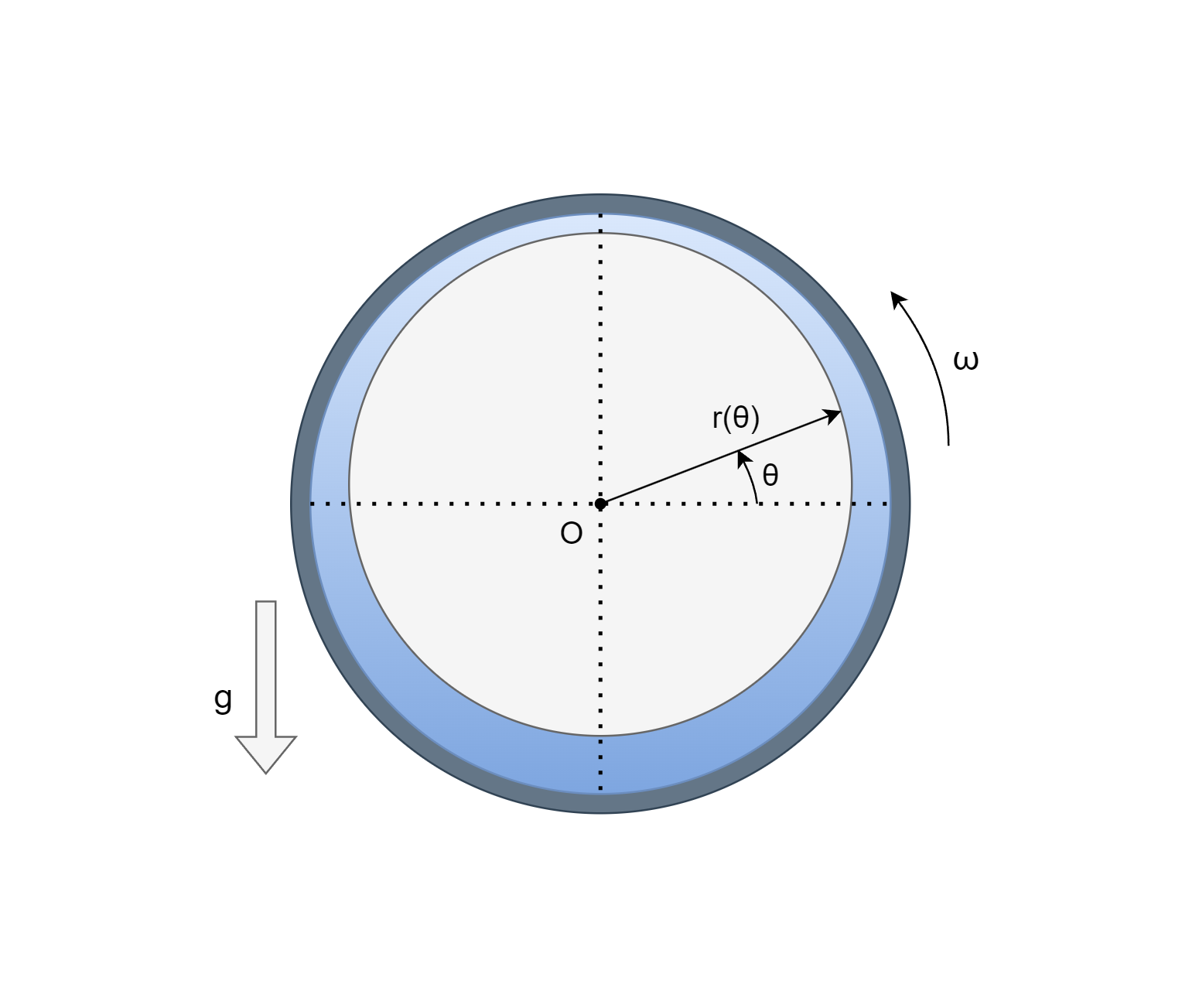
Ecoulement général

Notons que les approches qui suivent ne pourront pas décrire toutes les dynamiques du fluide tournant, qui change constamment de forme. Une analyse plus complète travaillerait en mécanique des fluides incluant à la fois viscosité, inertie et potentiels.

Le régime stationnaire hydrostatique

Un peu de mécanique sera donc de mise ! Supposons que le tube tourne dans des conditions telles qu'un régime hydrostatique stationnaire soit atteint, et que le fluide est parfait (supposition hautement douteuse puisqu'en général le spin-casting a pour but de répartir un fluide en cours de solidification).

Avec le repère circulaire tel que défini sur le schéma et un axe $z$ ascendant, étudions un point $M(r, \theta)$ à la surface libre du fluide. Les potentiels s'appliquant sur le fluide sont le potentiel centrifuge et le potentiel gravitationnel.

$$\begin{align*} \phi &= \phi_i + \phi_g \\\\ \phi &= \frac{\omega^2 r^2}{2} - g r \sin\theta \end{align*}$$

La surface est en état stationnaire donc équipotentielle :

$$\begin{align*} 0 &= \frac{d\phi}{d \theta} \\\\ 0 &= \omega^2r \frac{dr}{d\theta} - g\left(r \cos\theta + \frac{dr}{d\theta} \sin\theta \right) \end{align*}$$

En voilà une belle équation différentielle ordinaire ! Posons $A := \dfrac{g}{\omega^2}$. Notons d'ailleurs que $A<R$ lorsque l'effet centrifuge est assez fort pour assurer l'existence de liquide à la verticale : le fluide tourne assez vite pour compléter le "looping".

Cas des petites perturbations

Si les perturbations dues au poids sont faibles devant le rayon de la surface du fluide, on déduit l'équation simplifiée :

$$\begin{align*} 0 &= \frac{\partial r}{\partial \theta} - A \cos\theta \\\\ r &= R_0 + \frac{g}{\omega^2} \sin\theta \end{align*}$$

Quelle élégance !

Cas général

L'équation générale est bien délicate puisque non-homogène non linéaire à coefficients non constants. Néanmoins elle est du premier ordre et exacte. Il se trouve que l'on peut résoudre par une méthode intéressante. D'abord, réécrire sous forme la exacte :

$$\begin{align*} 0 = \left(A^{-1} r - \sin\theta\right)\cdot dr + \left(-r \cos\theta\right)\cdot d\theta \\\\ \text{avec} \space \frac{d\left(A^{-1} r - \sin\theta\right)}{\partial \theta} = \space \frac{d\left(-r \cos\theta\right)}{\partial r} = -\cos\theta \end{align*}$$

La solution d'une telle équation exacte est paramétrée par une variable $C \in \mathbb{R}$:

$$\begin{align*} &\begin{cases} C = \int \left(A^{-1} r - \sin\theta\right)\cdot dr + g(\theta) \\ C = \int \left(-r \cos\theta\right)\cdot d\theta + f(r) \end{cases} \\\\ &\begin{cases} C = \frac{A^{-1}}{2} r^2 -r \sin\theta + g(\theta) \\ C = f(r) -r \sin\theta \end{cases} \\\\ C &= \frac{A^{-1}}{2} r^2 -r \sin\theta \\\\ r &= A \left(\sin\theta \pm \sqrt{\sin^2\theta + \frac{4C}{A}}\right) \end{align*}$$

En évaluant en $\theta = 0$, on en déduit que la solution négative est irréalisable ($r < 0$). On pose $R_0 := \sqrt{4AC}$

$$\begin{align*} r &= R_0\cdot\sqrt{1 + \left(\frac{A}{R_0}\sin\theta\right)^2} + A \sin\theta \\\\ A &= \frac{g}{\omega^2} \end{align*}$$

Je trouve intéressant de voir le terme d'ordre 1 si clairement séparé alors que les ordres suivants (qui sont tous pairs !) sont issus de la même expression (la racine).

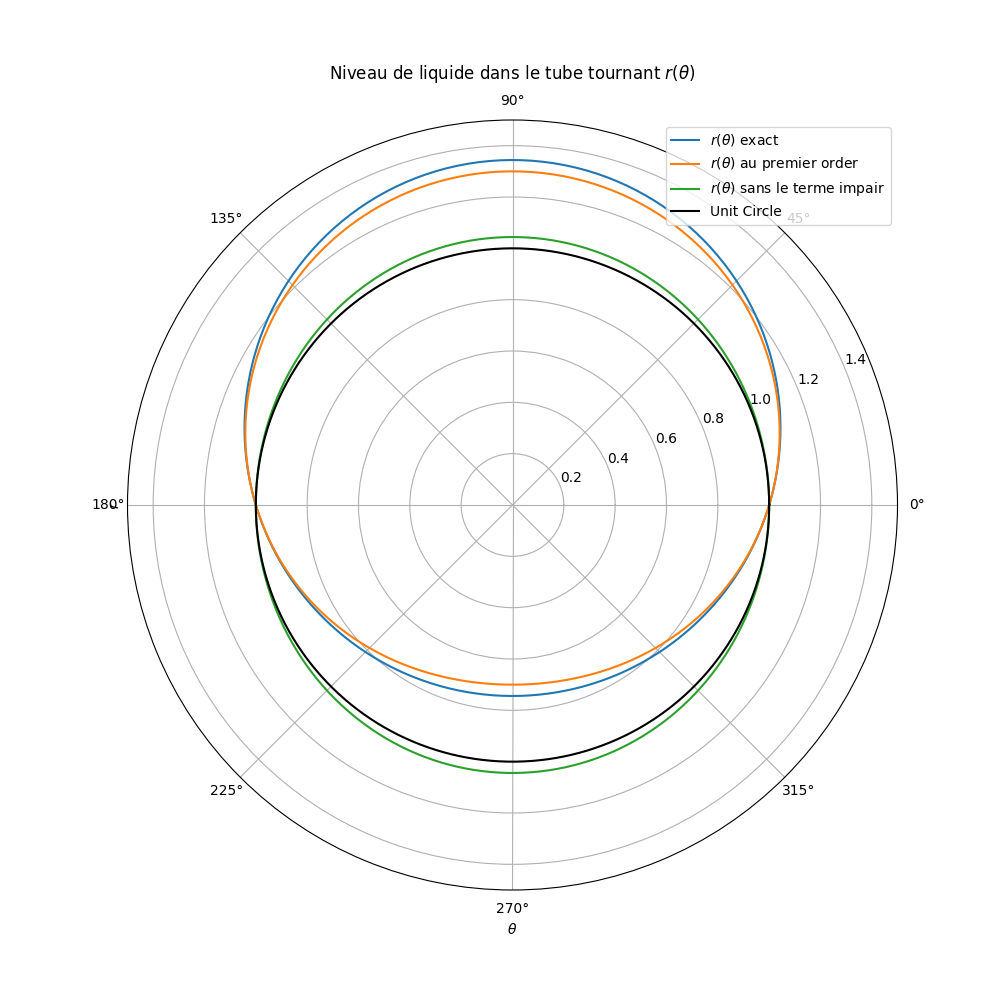
Lien avec les marée

C'est avec un certain effroi que je me rends compte que j'ai ici crée ce qui pourrait être un sujet de colle, de plus très calculatoire. Néanmoins, pour les nostalgiques de la prépa qui se rappellent de leurs cours sur les marées (petit rappel), nous avons globalement réalisé l'exercice avec une force centrale répulsive, et une perturbation uniforme, et nous trouvons tout de même un effet symétrique (ordre 2).

A l'inverse, notons que les marées ne présentent pas d'ordre premier, et pour une très bonne raison : l'ordre premier est impaire (merci Sherlock), et donc déplace le centre de masse du liquide. Cette perturbation dans le cadre des marrées est encodée dans le fait que les corps orbitent le barycentre du système.

Le régime stationnaire visqueux

attention

Ce paragraphe est hautement basé sur le théorème de l'espoir / le jugement, il convient de se limiter à des conclusions qualitatives.

En réalité, les fluides observés peuvent être en régime inertiel. $R\acute{e} = \dfrac{LV}{\nu} = \dfrac{L \cdot H \cdot \Omega}{\nu}$, où $H$ est la l'épaisseur de la couche de fluide, $L\approx R$ le rayon d'écoulement. Dans le cas de la marée, le nombre de Reynolds est grand. Dans un cas de spin-casting de liquide semblable à de l'eau, c'est toujours vrai : $L \approx 10^{-2}m$, $\Omega \approx 10^{2} rad/s, \nu \approx 10^{-6} m^2/s, H = 10^{-3}m$, $R\acute{e} \approx 10^{3}$.

Le régime visqueux est aussi possible. Les époxy par exemple, sont souvent assez visqueuses de l'ordre de quelques centaines de centipoises à quelques dizaines de milliers de centipoise. Or $1 cPs = 10^{-3} Pa\cdot s$. D'autres fluides pâteux seront plus visqueux encore. En supposant une densité proche de l'eau, la viscosité cinématique peut atteindre $\nu \approx 10^{-2} m^2/s$. Alors $R\acute{e} = 10^{-1}$, la viscosité est dominante.

D'accord, on peut avoir un écoulement, visqueux, et alors ?

Le cas visqueux est intéressant car il est certainement celui que le spin-caster expert rencontrera. Deux régimes sont possibles : si la rotation est lente par rapport au temps d'étalement d'un tas visqueux (je ne parle pas de goute car en mécanique des fluide l'étalement de la goutte est un problème de tension superficielle), le liquide se mélangera au fond, en mode bétonnière. Au contraire, si l'étalement est lent par rapport à la rotation, le fluide ne verra en moyenne que la "force" centrifuge, s'étalant.

Notons qu'il est fort possible que cette limite soit bien avant celle de $A<R$ trouvée dans le cas hydrostatique, assurant un spin-cast idéal à des vitesses plus faibles (!).

Temps d'écoulement

Raisonnons avec une combinaison d'analyse dimensionnelle et d'espoir naïf. Un tas en étalement sur le sol subis son poids et le frottement visqueux interne. On suppose l'écoulement visqueux donc ces forces sont à l'équilibre. Or la vitesse d'écoulement est proportionnelle à force visqueuse, donc au poids. On peut donc en déduire qu'il existe une constante $H [m]$ telle que :

$$V \propto \frac{g}{\nu}H^2$$

Cherchons donc une longueur pertinente caractéristique du système telle que $V \propto H^2$. Notons que la force de frottement est inversement proportionnelle à l'épaisseur d'écoulement, et que le poids est lui proportionnel à la masse au-dessus du système. Décidons donc que $H$ est la hauteur du tas.

Deux régimes

Le tas peut maintenant être placé, non plus sur le sol mais dans le tube pour être étalé. Le champ de gravité est remplacé par le champs de potentiel gravito-centrifuge $\phi = \phi_i + \phi_g$.

La bétonnière

Dans le cas où $V > \omega R$, le tas atteint l'équilibre au fond de la cuve dans un temps de l'ordre de la rotation. Si la "force" centrifuge ne domine pas la gravité, on constate une accumulation du fluide. $H$ reste donc grand, et la $V$ est maintenu: l'état est stable.

Le spin

Si $V < \omega R$, tout le contraire a lieu. L'étalement est assez lent pour que le tas commence à se circulariser, diminuant $H$. Cet état est aussi stable et tends vers $H = 0$. Notez qu'ainsi un même fluide dans un même tube tournant à la même vitesse peut s'étaler différemment selon son état initial. Pré étalez donc votre pâte !

info

L'absence de turbulences et une meilleure circularité quand la viscosité augmente est certainement la raison d'être du spin-casting !

Le mode "tas" n'existe donc plus dans ces conditions, mais bien sûr la perturbation ne disparait pas. La perturbation en mode "force" existe encore. Isolons l'hémicercle inférieur de fluide, fixe par rapport au laboratoire. Les échanges de matières sur ses bords se font vers le bas, et toujours dans l'hypothèse d'un écoulement purement visqueux, à une vitesse $dm \propto -\cos\theta$. Or, puisque le régime est stationnaire, une quantité égale de matière est perdue par différence de niveau de fluide. De tous les hémicercles, c'est celui qui gagne le plus de matière par écoulement, donc celui qui perd le plus de matière par différence de niveau de fluide. Donc le niveau de fluide est maximalement différent à l'horizontale !

Quantifier cette différence est non trivial puisqu'elle dépend de l'écoulement, et donc de l'épaisseur du fluide. On peut en revanche la savoir proportionnelle à $\dfrac{gH}{\nu}$ pour les couches minces puisque la vitesse découlement l'est, et à $\dfrac{1}{\omega}$ puisque l'accumulation de matière est l'intégrale de la vitesse, oscillant à la fréquence $\omega$. Il se trouve que l'on peut en faire un nombre adimensionné, rapport de l'effet de la gravité et de l'écoulement visqueux :

$$Ks = \dfrac{g}{\omega} \dfrac{H}{\nu}$$

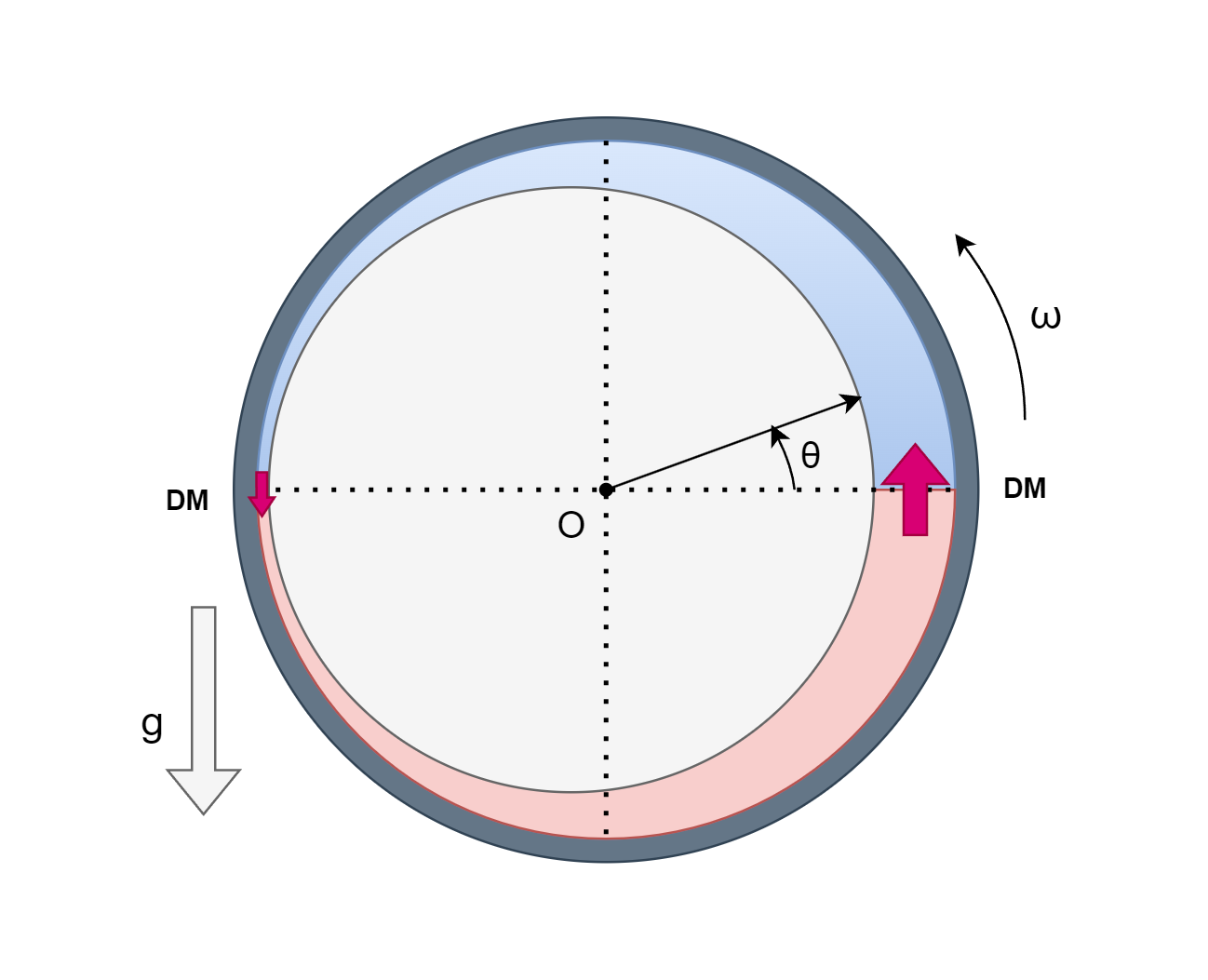
Retard de phases

Nous avons étudié 3 régimes bien distincts. En considérant le système comme un fluide tournant circulaire perturbé sinusoïdalement, nous avons vu :

Cas	Retard de phase	Interprétation
Hydrostatique à l'ordre 1	$0°$	Le fluide est toujours au fond du puis de potentiel.
Visqueux bétonnière	$[-180°,0°]$	Le fluide d'accumule lors de la phase montante, ou il reste, équilibrante la viscosité et le poids. Il suit la perturbation en mode "tas"
Visqueux spin	$\infty \space \& \space -90°$	Le fluide ne suit pas la perturbation en mode "tas", mais la perturbation en mode "force" existe et est en quadrature retard.

Conclusions

Le spin-casting est loin d'être un problème physique simple ! Son application est pourtant directe et utile, n'hésitez, pas spinez !